Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter5: Inverse, Exponential, And Logarithmic Functions
Section5.2: Exponential Functions
Problem 3E
Related questions
Question
Solve using the

Transcribed Image Text:08 - Rational Fractions.pdf
5
MADE4Learners
FRAMEWORK
Math138 - Engineering Calculus 2
1
How to resolve a proper rational fraction into its partial fractions.
If a linear factor ax + b occurs once as a factor of the
denominator, there corresponds to this factor a partial fraction
of the from
where A is a constant to be determined.
A
ax+b'
• If a linear factor ax + b occurs n times as a factor of the
denominator, there corresponds to this factor ʼn partial fractions
in the form
A₁
A₂
An
+
ax + b (ax + b)²
(ax + b)n
where A's are constants to be determined.
MADE4Learners
FRAMEWORK
Math138 - Engineering Calculus 2
2
● If an irreducible (not factorable) quadratic factor ax² + bx + c
occurs once as a factor in the denominator, there corresponds to
this factor one partial fraction in the form A(2ax+b)+B, where A
and B are constants to be determined and 2ax + b is the
derivative of ax² + bx + c.
ax²+bx+c ¹
● If an irreducible (not factorable) quadratic factor ax² + bx+c
occurs n times as a factor in the denominator, there corresponds
to this factor n partial fractions in the form
A₁ (2ax + b) + B₁,
ax² + bx + c
+
A₂(2ax + b) + B₂
(ax² + bx + c)²
+
An(2ax + b) + Bn
(ax²+bx+c)n
where A's and Bi's are constants to be determined and 2ax + b
is the derivative of ax² + bx + c.
3
Sac
Math138 - Engineering Calculus 2
3
How to solve the constants?
✪ By assigning a particular value to x so that some of the

Transcribed Image Text:S
x²-x+1
x² + 2x + 2
-dx
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Can you solve using the same method shown on the first picture please
![2x-10
dx
= ( ( + = 1/5 ) dx
X-3
= 12/1dx - 12/²3 dx
= In
• 3 ³ /x + ₁] - √n / x - 3] + C ]
2x-10
(x+1)(x-3)
2x-10
(X+1)(x-3)
2x-10
Let x= -1
->
A
B
t
X + 1
X-3
A (x-3) + B(x+1)
(x+1) (x-3)
A (X-3) + B(x+1)
2(-1)-10 = A (-1-3) + B (-1+1)
-12-4 A
A = 3
H
Let x = 3
2 (3)-10= A (3-3) + B (3-1)
- 4 = 48
B = -.](https://content.bartleby.com/qna-images/question/874771a1-bb33-4831-94bb-e08e7361cdee/5a2ae513-537b-44d0-bba2-c58e8be74831/kqrihn5_thumbnail.jpeg)
Transcribed Image Text:2x-10
dx
= ( ( + = 1/5 ) dx
X-3
= 12/1dx - 12/²3 dx
= In
• 3 ³ /x + ₁] - √n / x - 3] + C ]
2x-10
(x+1)(x-3)
2x-10
(X+1)(x-3)
2x-10
Let x= -1
->
A
B
t
X + 1
X-3
A (x-3) + B(x+1)
(x+1) (x-3)
A (X-3) + B(x+1)
2(-1)-10 = A (-1-3) + B (-1+1)
-12-4 A
A = 3
H
Let x = 3
2 (3)-10= A (3-3) + B (3-1)
- 4 = 48
B = -.
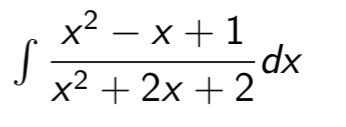
Transcribed Image Text:S
x²-x+1
x² + 2x + 2
-dx
Solution
Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning