4. (a) Find a differential equation to model the velocity v of a falling mass m as a function of time. Assume that air resistance is proportional to the instantaneous velocity, with a constant of proportionality k > 0 (this is called the drag coefficient). Take the downward direction to be positive. (b) Solve the differential equation subject to the initial condition v(t = 0) = vo. (c) Determine the terminal velocity of the mass.
4. (a) Find a differential equation to model the velocity v of a falling mass m as a function of time. Assume that air resistance is proportional to the instantaneous velocity, with a constant of proportionality k > 0 (this is called the drag coefficient). Take the downward direction to be positive. (b) Solve the differential equation subject to the initial condition v(t = 0) = vo. (c) Determine the terminal velocity of the mass.
Principles of Heat Transfer (Activate Learning with these NEW titles from Engineering!)
8th Edition
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Kreith, Frank; Manglik, Raj M.
Chapter5: Analysis Of Convection Heat Transfer
Section: Chapter Questions
Problem 5.33P
Related questions
Question

Transcribed Image Text:4. (a) Find a differential equation to model the velocity v of a falling mass m as a function of
time. Assume that air resistance is proportional to the instantaneous velocity, with a
constant of proportionality k > 0 (this is called the drag coefficient). Take the downward
direction to be positive.
(b) Solve the differential equation subject to the initial condition v(t = 0) = vo.
(c) Determine the terminal velocity of the mass.
Expert Solution
Step 1
Given, mass of the object = m.
Let 'v' be the instantaneous velocity of the object free falling.
Air resistance is assumed proportional to instantaneous velocity as: ; where is the proportionality constant.
(a) Free body diagram of the falling mass is drawn below.
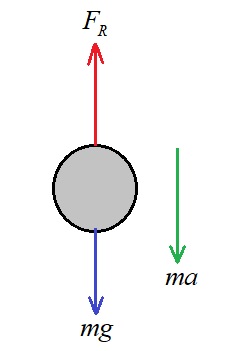
Here, ; where acceleration of the mass,
------------------------------ (1)
Equation (1) represents the differential equation to model velocity (v) of falling mass (m).
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Principles of Heat Transfer (Activate Learning wi…
Mechanical Engineering
ISBN:
9781305387102
Author:
Kreith, Frank; Manglik, Raj M.
Publisher:
Cengage Learning

Principles of Heat Transfer (Activate Learning wi…
Mechanical Engineering
ISBN:
9781305387102
Author:
Kreith, Frank; Manglik, Raj M.
Publisher:
Cengage Learning